Materi Lengkap Rumus Bangun Datar dan Bangun Ruang

Pada mata kuliah algoritma dan pemrograman terstruktur materi awal yang dipelajari adalah bangun ruang dan bangun datar. Hal ini bertujuan untuk mengetahui rumus-rumus bangun ruang dan bangun datar untuk diterapkan ke dalam flowchart sebelum implementasikan ke dalam suatu program menggunakan bahasa programming tertentu.

Menghitung luas dan keliling bangun datar merupakan salah satu materi dasar dalam ilmu matematika. Mulai dari Sekolah Dasar sampai SMP, SMA, bahkan sampai perguruan tinggi (university) khususnya jurusan matematika, bangun datar merupakan materi dasar yang harus dikuasai.

Bangun datar adalah bangun yang datar berbentuk 2D yang memiliki ukuran panjang x lebar yang umumnya dicari adalah luas dan keliling bangun datar.

Bangun Datar Lengkap

1. Persegi
2. Persegi Panjang
3. Segitiga
4. Jajar Genjang
5. Trapesium
6. Lingkaran
7. Belah Ketupat
8. Layang-layang

Untuk menghitung luas dan keliling dari sebuah bangun datar, seperti segitiga, persegi empat, jajargenjang, trapesium, dan lain-lain, kita memerlukan tools yang disebut rumus (formula). Nah, langsung saja berikut kumpulan rumus-rumus lengkap untuk menghitung luas dan keliling bangun datar lengkap dengan gambarnya.

Rumus bangun datar

1. PERSEGI

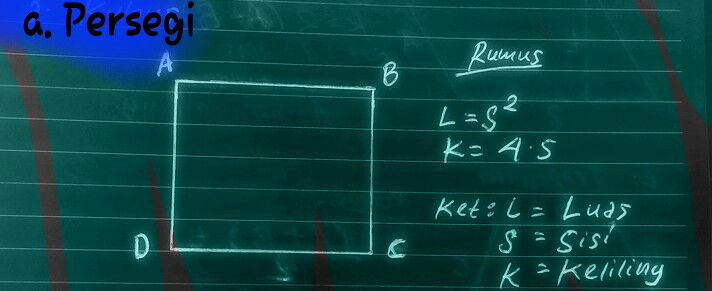
a. Gambar bangun datar persegi

Keunikan dan sifat-sifat persegi:

1. Memiliki 4 sisi
2. Setiap sisi persegi sama panjang
3. Memiliki 4 sudut yang besarnya 90º

RUMUS PERSEGI:

LUAS=sisi X sisi
KELILING=4 X sisi

Contoh soal mencari luas dan keliling persegi

Sebuah lantai berbentuk persegi memiliki sisi 20 cm. Hitunglah keliling dan luas lantai tersebut!

jawab:
Diketahui s=20 cm
Ditanyakan: keliling dan luas persegi?

luas persegi = sisi X sisi
20 cm X 20 cm = 400 cm²

keliling persegi = 4 X sisi
4 X 20 cm = 80 cm

Jadi, keliling persegi tersebut adalah 80 cm dan luasnya 400 cm.

2. PERSEGI PANJANG

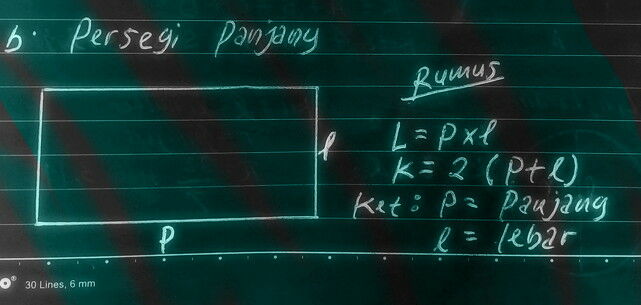
b. Gambar bangun datar persegi panjang

Keunikan dan sifat-sifat persegi panjang:

1. Memiliki 2 sisi lebar sama panjang
2. Memiliki 2 sisi panjang yang sama panjang
3. Memiliki 4 sudut yang besarnya 90º

RUMUS PERSEGI PANJANG:

LUAS = p X l
KELILING = 2 (p + l)

NB: p = panjang dan l = lebar.

Contoh soal menghitung luas dan keliling persegi panjang

Sebuah lapangan sepak bola memiliki panjang 100 m dan lebar 60 m. Tentukan luas dan keliling lapangan bola tersebut!

jawab:

Diketahui: p = 100 m
l = 60 cm
Ditanyakan: keliling dan luas lapangan sepak bola?

luas persegi panjang = p X l
100 m X 60 m = 600 m²

keliling persegi panjang = 2 X (p + l)
2 X (100 m + 60 m) = 320 m

Jadi, lapangan bola tersebut memiliki keliling 320 m dan luasnnya 600 m².

3. SEGITIGA

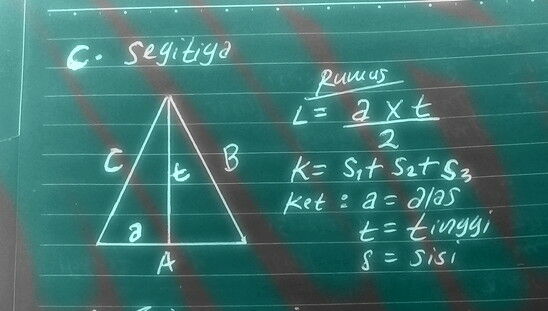
c. Gambar bangun datar segitiga

Keunikan dan sifat segitiga:

1. Memiliki 3 sisi
2. Memiliki 4 jenis bentuk, yaitu segitiga siku-siku, segitiga sama sisi, segitiga sembarang, dan segitiga sama kaki.
3. Segitiga siku-siku besar salah satu sudutnya 90º (rumus pythagoras)

RUMUS SEGITIGA:

LUAS= 1/2 a X t
KELILING=sisi + sisi + sisi

NB: a = alas segitiga, t = tinggi segitiga

Contoh soal menghitung luas dan keliling segitiga

Hitunglah keliling dan luas segitiga sama sisi yang memiliki panjang sisi 8 cm!

luas segitiga = 1/2 a X t
1/2 (8 cm X 8 cm)
1/2 64 cm = 32 cm²

keliling segitiga = sisi + sisi + sisi
8 cm + 8cm + 8 cm = 24 cm

Jadi, keliling segitiga sama kaki tersebut adalah 24 cm dan luasnya 32 cm².

4. JAJAR GENJANG

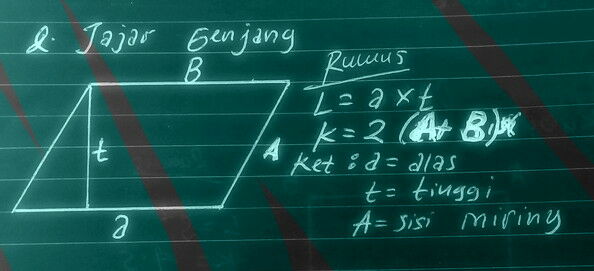
d. Gambar bangun datar jajar genjang

RUMUS JAJAR GENJANG:

LUAS= a X t
KELILING= 2 (a + b)

Keunikan dan sifat-sifat jajargenjang

1. Memiliki 2 pasang sisi sejajar
2. Memiliki 4 sisi

Contoh soal menghitung luas dan keliling jajargenjang

Sebuah bangun datar jajargenjang ABCD dengan keterangan AB=DC = 5 cm dan sisi AD=BC = 7 cm dan tinggi jajargenjang 10 cm. Hitunglah luas dan keliling jajargenjang tersebut jika alasnya adalah sisi AB!

jawab
Diketahui AB=DC = 5 cm
AD=BC = 7 cm
t = 10 cm
Ditanyakan luas dan keliling?

luas = a X t
5 cm X 7 cm = 35 cm²

keliling = 2 (AB + AD)
2 (5 cm + 7 cm) = 24 cm

Jadi, keliling jajargenjang ABCD adalah 24 cm dengan luasnya 35 cm².

5. TRAPESIUM

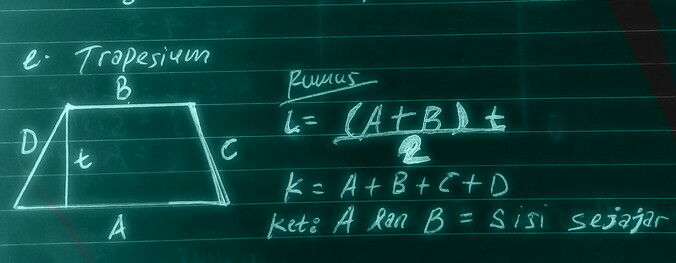
e. Gambar bangun datar trapesium

Keunikan dan sifat-sifat trapesium
1. Memiliki 4 sisi

RUMUS TRAPESIUM

LUAS=1/2 (A + B) X t
KELILING=A+B+C+D

NB: Perhatikan gambar trapesium di atas. A dan B adalah sisi sejajar.

6. LINGKARAN

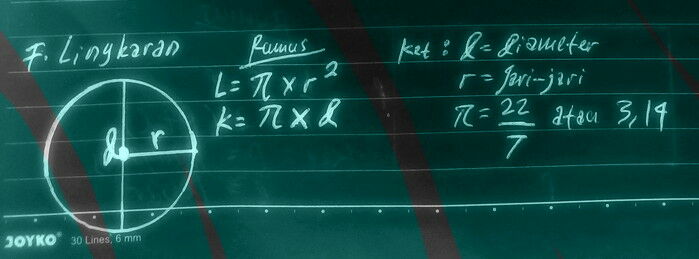
f. Gambar bangun datar lingkaran

RUMUS LINGKARAN:

LUAS=π X r²
KELILING=2π X r

NB: π = 22/7 atau 3,14
r = jari-jari = 1/2 diameter
diameter = d = 2 X r

7. BELAH KETUPAT

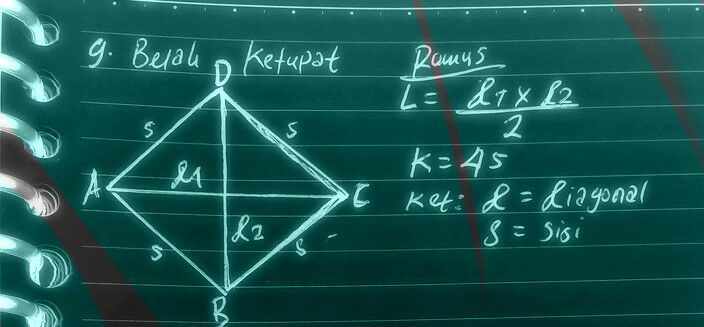
g. Gambar bangun datar belah ketupat

Keunikan bangun belah ketupat
1. Memiliki 4 sisi sama panjang
2. Sama dengan persegi

RUMUS BELAH KETUPAT

LUAS=(d1 + d2) /2
KELILING=4S

NB: Perhatikan gambar bangun belah ketupat di atas!
d = diagonal, S = sisi

8. LAYANG-LAYANG

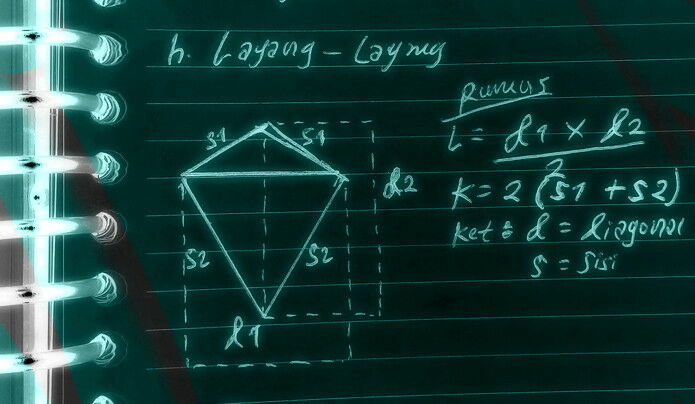
h. Gambar bangun datar layang-layang

RUMUS LAYANG-LAYANG

LUAS=(d1 + d2) /2
KELILING=2 (s1 + s2)

NB: Perhatikan gambar layang-layang di atas!
d = diagonal, s = sisi

Rumus menghitung luas dan keliling bangun datar di atas, merupakan suatu ketentuan yang tidak akan pernah berubah dan akan terus digunakan. Jika anda memahami rumus bangun datar di atas maka anda akan lebih mudah mempelajari rumus bangun ruang. Sedikit informasi, bangun ruang dibentuk dari gabungan beberapa bangun datar.

Dalam kehidupan sehari-hari, kemampuan menghitung luas bangun datar dapat diaplikasikan kedalam menghitung luas suatu perumahan, menghitung luas area persawahan, dan masih banyak lagi.

NB: Ilmu matematika sangat dekat dengan kehidupan manusia yang sering kita hiraukan begitu saja, termasuk pelajaran tentang bangun datar ini.

Demikianlah rumus matematika menghitung luas dan keliling bangun datar lengkap. Selain bangun datar, dalam ilmu matematika juga terdapat materi lanjutan tentang bangun, yaitu materi bangun ruang .

Dalam dunia matematika suatu bidang ilmu atau materi merupakan lanjutan dari materi sebelumnya atau dengan kata lain materi sebelumnya yang kita pelajari memiliki hubungan dengan materi selanjutnya.

Seperti halnya dalam mata kuliah algoritma dan pemrograman terstruktur dan di jenjang-jenjang pendidikan sebelumnya, materi bangun ruang merupakan materi lanjutan dari bangun datar dalam ilmu matematika.

Sesuai dengan namanya, bangun ruang berbentuk tiga dimensi (3D) yang memiliki ruang didalamnya.

Dalam pendidikan seni dan budaya, kita dapat dengan mudah dapat membedakan antara karya 2D dan karya 3D. Karya 2D contohnya lukisan pada kanvas dan karya 3D contohnya patung yang di pahat dari kayu.

Seperti contoh dalam pendidikan seni budaya di atas, dalam dunia matematika, bangun ruang dan bangun datar juga sangat mudah di bedakan. Bangun datar hanya memiliki ukuran panjang dan lebar (luas) sedangkan bangun ruang memiliki ukuran panjang, lebar, dan tinggi (volume).

Bangun ruang lengkap

1. Kubus
2. Balok
3. Bola
4. Tabung atau silinder
5. Kerucut
6. Limas segiempat
7. Prisma segitiga

Jika diperhatikan dengan seksama, dalam ilmu matematika bangun ruang dibentuk dari gabungan bangun datar. Misalnya kubus dibentuk dari persegi, bola dibentuk dari lingkaran, limas segi empat dibentuk dari persegi dan segitiga, dan lain sebagainya. Langsung saja, berikut gambar rumus bangun ruang lengkap dalam matematika.

Rumus bangun ruang

1. Kubus

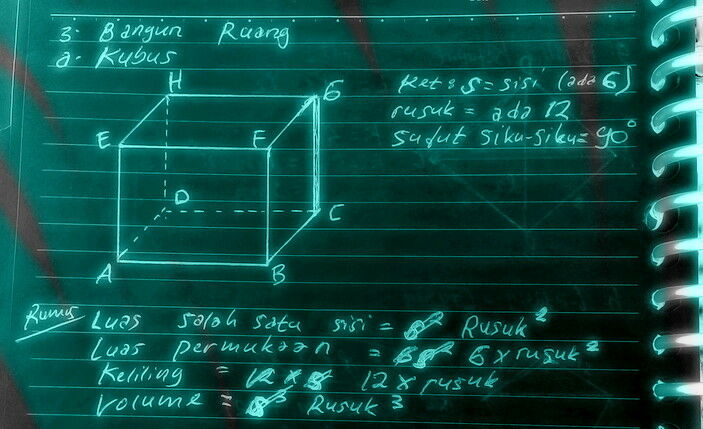
a. Gambar bangun ruang kubus

Keunikan dan sifat-sifat kubus

1. Memiliki 6 sisi yang dibangun dari gabungan bangun datar persegi
2. Memiliki 12 rusuk yang sama panjang
3. Semua sudut besarnya 90º
4. Memiliki 8 titik sudut

RUMUS KUBUS

LUAS SALAH SATU SISI=rusuk X rusuk
LUAS PERMUKAAN KUBUS=6 X rusuk X rusuk
KELILING KUBUS=12 X rusuk
VOLUME KUBUS=rusuk X rusuk X rusuk (r^3)

2. Balok

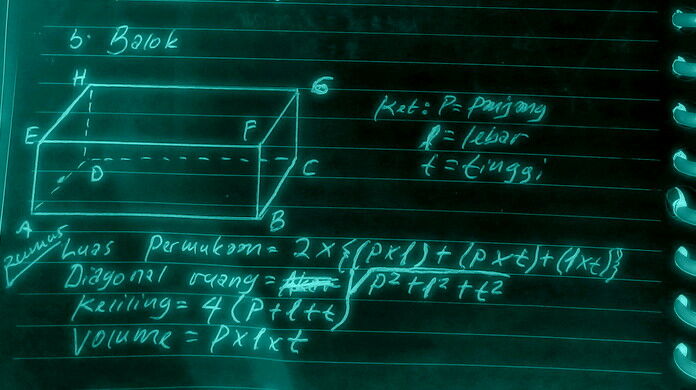
b. Gambar bangun ruang balok

Keunikan dan sifat-sifat balok

1. Memiliki 6 sisi yang dibangun dari gabungan bangun persegi panjang
2. Semua sudut besarnya 90º
3. Memiliki 8 titik sudut

RUMUS BALOK

LUAS PERMUKAAN BALOK=2 X {(p X l) + (p X t) + (l X t)}
DIAGONAL RUANG=AKAR (p² + l² + t²)
KELILING BALOK=4 (p + l + t)
VOLUME BALOK=p X l X t

NB: p = panjang, l = lebar, t = tinggi

3. Bola

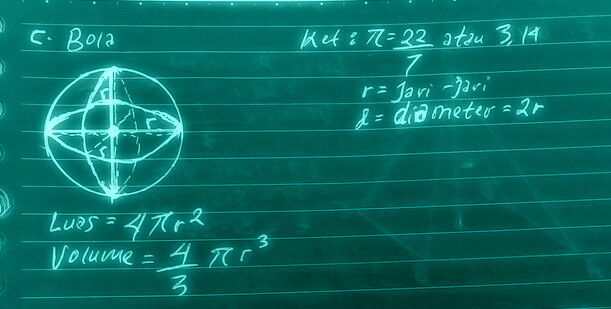
c. Gambar bangun ruang bola

Keunikan dan sifat-sifat bola

1. Bola dibangun dari 4 bangun datar lingkaran
2. Memiliki sudut 360º

RUMUS BOLA

LUAS BOLA=4 π r²
VOLUME BOLA=4/3 π r³

NB: π = 22/7 atau 3.14
r = jari-jari = 1/2 d
d= diameter = 2 X r

4. Tabung/silinder

d. Gambar bangun ruang tabung/silinder

Keunikan dan sifat-sifat tabung

1. Bangun tabung terdiri dari 2 lingkaran dan 1 persegi panjang

RUMUS TABUNG

LUAS PERMUKAAN=2 π r (r + t)
VOLUME TABUNG=π r² t
LUAS SELIMUT TABUNG=2 π r t

NB: r= jari-jari, t= tinggi tabung, dan h= selimut

5. Kerucut

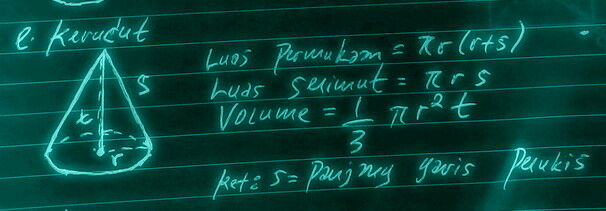
e. Gambar bangun ruang kerucut

Keunikan dan sifat-sifat kerucut

1. Bangun kerucut merupakan bentuk dari 1/3 tabung

RUMUS KERUCUT

LUAS PERMUKAAN=π r (r + s)
LUAS SELIMUT=π r s
VOLUME KERUCUT=1/3 π r² t

NB: r= jari-jari, s=panjang garis pelukis, dan t=tinggi kerucut

6. Limas

f. Gambar bangun ruang limas

Keunikan dan sifat-sifat llimas segiempat

1. Bangun limas terdiri dari 4 bangun segitiga sebagai sisi
2. Bangun ruang limas menggunakan bangun persegi sebagai alas
3. Bangun limas merupakan 1/3 dari kubus

RUMUS LIMAS

LUAS PERMUKAAN=Luas alas + jumlah luas sisi tegak
LUAS PERMUKAAN=s² + 4 (1/2 a X t)

VOLUME LIMAS=1/3 Luas alas x T
VOLUME LIMAS=1/3 s² X T

NB:
1. Luas alas limas=rumus luas bangun datar persegi
2. Jumlah luas sisi tegak= rumus luas segitiga= 1/2 (a X t)
3. T= tinggi limas
4. t= tinggi segitiga

7. Prisma

g. Gambar bangun ruang prisma

Keunikan dan sifat-sifat prisma (khusus prisma segitiga)

1. Prisma segitiga merupakan 1/2 dari bangun ruang balok
2. Prisma segitiga terdiri dari 2 sisi segitiga dan 3 sisi persegi panjang
3. Prisma segiempat sama dengan bangun balok

RUMUS PRISMA SEGITIGA

LUAS PERMUKAAN=(2 X luas alas) + (k X T)
LUAS PERMUKAAN=(a X t) + (k X T)

VOLUME PRISMA=Luas alas X T
VOLUME PRISMA=1/2 (a X t X T)

NB:
1. Luas alas prisma= luas segitiga=1/2 (a X t)
2. k = keliling alas
3. T =tinggi prisma
4. t = tinggi segitiga

Jika kita memahami keunikan-keunikan dan sifat-sifat bangun ruang di atas, kita dapat dengan mudah menghafal rumus-rumusnya, baik itu rumus volume bangun ruang maupun rumus luas permukaan bangun ruang. Sekali lagi, bangun ruang dibentuk dan dibangun dari gabungan beberapa bangun datar.

Dalam kehidupan sehari-hari, menghitung volume bangun ruang dapat diaplikasikan ketika menghitung volume air di dalam sebuah kolam, dan masih banyak lagi kegunaan ilmu matematika yang satu ini.

Demikianlah artikel lengkap tentang rumus luas dan keliling bangun datar dan rumus luas permukaan dan volume bangun ruang beserta gambar bangun ruang dalam matematika. Semoga bermanfaat!

Rumus bangun datar dan bangun ruang