Himpunan

Materi Himpunan Lengkap

MK logika informatika" setelah pada pelajaran pertama kita belajar tentang logika matematika pada mata kuliah logika informatika, kita masuk ke pelajaran yang kedua yaitu himpunan, relasi, dan fungsi.

Pengertian Himpunan

Himpunan adalah kumpulan benda-benda atau objek yang dapat didefinisikan (diterangkan) dengan jelas. Nama himpunan ditulis dengan huruf kapital dan diapit oleh tanda kurung kurawal.

Jenis-jenis Himpunan

1. Himpunan sama

Himpunan sama adalah himpunan yang memiliki elemen-elemen yang sama. Himpunan sama tidak mempengaruhi kesamaan dua himpunan dari segi urutan dan pengulangan dan berlaku sifat aksioma untuk tiga atau lebih himpunan.

A={1, 2, 3}
B={1, 3, 2}

2. Himpunan terpisah

Himpunan terpisah atau himpunan saling lepas karena masing-masing himpunan tidak memiliki anggota himpunan yang sama.

A={1, 2}
B={3, 4}

3. Himpunan bagian

Himpunan bagian atau himpunan subset adalah himpunan yang memiliki semua anggota suatu himpunan.

A={1, 3, 5}
B={1, 3, 5, 7}

Dari data himpunan di atas, semua elemen himpunan A termuat dalam elemen himpunan B sehingga himpunan A merupakan himpunan bagian dari himpunan B. Jadi, B merupakan superset dari A.

4. Himpunan kosong

Himpunan kosong adalah himpunan yang tidak memiliki satu pun elemen himpunan dengan kardinalitas = 0. Himpunan kosong berbeda dengan himpunan yang memiliki hasil 0.

Jika diketahui:
A={1, 3, 5,}
B={3, 5, 7}
Tentukan bilangan genap yang ada?
Jawabannya : {}

5. Himpunan berhingga

Himpunan berhingga adalah himpunan yang memiliki anggota-anggota dengan jelas dan dapat didefinisikan sesuai dengan petunjuk yang disediakan.

Contoh himpunan berhingga:

Himpunan A adalah nama-nama hari dalam satu minggu.
A={Senin, Selasa, Rabu, Kamis, Jumat, Sabtu, Minggu}

Himpunan A di atas disebut himpunan berhingga karena memiliki anggota-anggota yang jelas dan dapat didefinisikan, yaitu nama-nama ghari dalam satu minggu.

6. Himpunan tak berhingga

Himpunan tak berhingga adalah himpunan yang anggota-anggotanya tidak dapat didefinisikan dengan jelas karena petunjuk pendefinisian yang kurang akurat.

Contoh himpunan tak berhingga:

Himpunan A adalah himpunan bilangan prima
A={2, 3, 5, 7, ...}

Himpunan A di atas disebut himpunan tak berhingga karena anggota-anggotanya tidak dapat didefinisikan dengan pasti, yaitu batas bilangan prima yang dimaksud.

7. Himpunan ekuivalen

Himpunan ekuivalen adalah himpunan yang memiliki jumlah elemen yang sama meskipun anggota-angotanya berbeda.

A={a, b, c}
B={1, 2, 3}

Dari data himpunan di atas, himpunan A dan himpunan B merupakan ekuivalen karena memiliki jumlah anggota yang sama, yaitu masing-masing 3 anggota.

Contoh Himpunan bilangan

Ada berbagai macam himpunan di dunia ini. Namun himpunan dalam dunia matematika yang wajib anda ketahui adalah himpunan bilangan. Hal ini mutlak harus anda pahami, khususnya pada materi himpunan ini sering muncul soal yang meminta anda mendefinisikan jenis-jenis bilangan tertentu.

Jenis-jenis bilangan

1. Himpunan bilangan asli/real

R={1, 2, 3, 4, 5, 6, 7, ...}

2. Himpunan bilangan cacah

C={0, 1, 2, 3, 4, 5, 6, 7,...}

3. Himpunan bilangan prima

P={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...}

4. Himpunan bilangan ganjil

L={1, 3, 5,7, 9, 11, ...}

5. Himpunan bilangan bulat

B={ .., -2, -1, 0, 1, 2, 3, ...}

6. Himpunan bilangan genap

N={2, 4, 6, 8, 10, 12, ...}

7. Himpunan bilangan rasional

Q={x | x = a/b, a dan b ∑ B, b ≠ 0}

Cara Penyajian Himpunan

1. Notasi Pembentuk Himpunan

Penyajian himpunan dengan metode notasi pembentuk himpunan adalah penyajian himpunan yang dilakukan dengan cara mendefinisikan terlebih dahulu anggota-anggota suatu himpunan dalam bentuk variabel untuk dapat mengetahui anggota-anggota dalam himpunan tersebut.

Setelah mendefinisikan variabel, anggota-anggota suatu himpunan akan diketahui dan diubah ke dalam metode penyajian pendaftaran atau tabular dengan maksud memudahkan pembaca himpunan. Berikut beberapa contoh penyajian dalam metode notasi pembentuk himpunan.

a. A={x | x adalah huruf vokal dalam abjad}

Cara baca: x adalah anggota himpunan A, dimana x adalah huruf vokal dalam abjad.

b. B={x | x adalah 5 hewan berkaki empat yang dimulai dari huruf k}

c. C={x | x < 10, x ∑ bilangan prima}

Cara baca: x adalah anggota himpunan C, dimana x kurang dari 10, dan x elemen bilangan prima.

d. D={x | x ≤ 11, x ∑ bilangan prima}

Cara baca: x adalah anggota himpunan D, dimana x kurang atau sama dengan 11, dan x eleman bilangan prima}

e. E={x | -3 < x < 4, x ∑ bilangan bulat}

Cara baca: x adalah anggota himpunan E, dimana x tidak kurang -3 dan tidak lebih dari 4, dan x elemen bilangan bulat.

f. F={x | 10 < x < 20, x ∑ bilangan prima}

Cara baca: x adalah anggota himpunnan F, dimana x tidak kurang dari 10 dan tidak lebih dari 20, dan x elemen bilangan prima.

Anggota-anggota di atas masih dalam bentuk notasi pembentuk himpunan dan untuk dapat melihat anggota-anggota himpunannya dengan lebih jelas maka harus didefinisikan ke dalam bentuk pendaftaran.

2. Pendaftaran (tabular)

Penyajian himpunan dengan metode pendaftaran atau tabular adalah penyajian himpunan secara langsung dengan menunjukkan anggota-anggota himpunan dalam suatu himpunan. Berikut beberapa contoh penyajian himpunan dengan metode pendaftaran.

a. A={a, i, u, e, o}

b. B={kuda, kambing, kerbau, kijang, kelinci}

c. C={2, 3, 5, 7,}

d. D={2, 3, 5, 7, 11}

e. E={-2, -1, 0, 1, 2, 3}

f. F={11, 13, 17, 19}

Operasi Himpunan dengan Diagram Venn

1. Irisan

A ∩ B={x | x ∑ A, x ∑ B}

Irisan adalah anggota-anggota himpunan yang sama dan terletak di semua himpunan yang ada.

A={1, 2, 3, 4}
B={1, 3, 5, 6}

A ∩ B={1, 3}

2. Gabungan

A U B={x | x ∑ A, x ∑ B}

Gabungan adalah gabungan anggota himpunan dari semua himpunan yang ada.

A={1, 3, 5, 7}
B={2, 3, 4, 5, 6}

A U B={1, 2, 3, 4, 5, 6, 7}

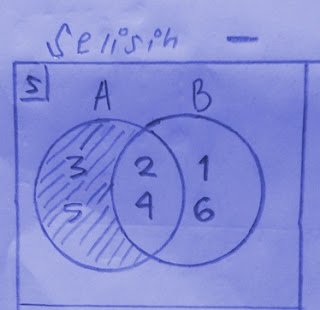
3. Selisih

A - B={x | x ∑ A, x “I” B}

Selisih adalah anggota himpunan A yang tersisa setelah dikurangi oleh anggota himpunan B atau dengan kata lain yang himpunan A yang tidak termasuk himpunan B.

A={2, 3, 4, 5}
B={1, 2, 4, 6}

A - B={3, 5}

B - A={1, 6}

4. Komplemen

A’={x | x ∑ S, x “I” A}

Komplemen adalah semua anggota di luar anggota himpunan yang disebutkan atau dengan kata lain komplemen merupakan anggota yang bukan jawaban dari suatu operasi. Komplemen erat hubungannya dengan semesta. Semesta adalah semua gabungan anggota dari himpunan-himpunan yang ada.

S={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A={3, 4, 6, 7, 9}
B={3, 5, 7, 9, 10}

(A U B)’={1, 2, 8}

A’={1, 2, 5, 8, 10}
B’={1, 2, 4, 6, 8}

Contoh soal himpunan dan jawabannya

Untuk lebih memahami konsep dari materi himpunan ini, silahkan menyimak contoh-contoh soal himpunan di bawah lengkap dengan contohnya.

1. Nyatakan himpunan berikut ke dalam bentuk notasi pembangun himpunan (set builder form)

a. A={5, 10, 15, 20, 25}

Jawab:

A={x | 5 ≤ x ≤ 25, x ∑ bilangan asli kelipatan 5}

b. B={0, 1, 2, 3, 4, 5}

Jawab:

B={x | x ≤ 5, x ∑ bilangan cacah}

c. C={-1. 0, 1, 2, 3}

Jawab:

C={x | -1 ≤ x ≤ 3, x ∑ bilangan bulat}

2. Diketahui data-data sebagai berikut.

S={x|x adalah 5 huruf vokal dalam abjad}
A={x|x adalah huruf vokal dalam kata “informatika”}
B={x|x adalah huruf vokal dalam kata “matematika”}
C={x|x adalah huruf vokal dalam kata “kuis”}

Tentukan operasi himpunan berikut dan gambarkan diagram venn-nya.

S={a, i, u, e, o}
A={i, o, a}
B={a, e, i}
C={u, i}

a. A - C

A - C={o, a}

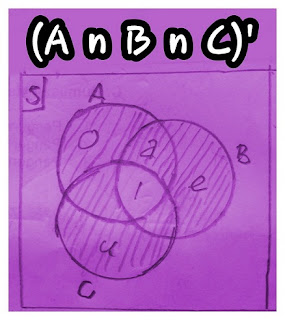
b. (A U B)’

(A U B)’={u}

c. A ∩ B ∩ C

A ∩ B ∩ C={i}

d. A U B U C

A U B U C={a, i, u, e, o}

e. (A ∩ B ∩ C)’

(A ∩ B ∩ C)’={a, u, e, o}

3. Diketahui data-data sebagai berikut.

A={b, c}
B={1, 3, 5}
C={2, 3, 5}

Tentukan operasi himpunan berikut.

a. A X (B U C)

(B U C)={1, 2, 3, 5}

A X (B U C)={(1, b), (1, c), (2, b), (2, c), (3, b), (3, c), (5, b), (5, c)

b. (A X B) ∩ (A X C)

(A X B)={(1, b), (1, c), (3, b), (3, c), (5, b), (5, c)}
(A X C)={(2, b), (2, c), (3, b), (3, c), (5, b), (5, c)}

(A X B) ∩ (A X C)={(3, b), (3, c), (5, b), (5, c)}

4. Tentukan anggota himpunan dari operasi-operasi himpunan berikut!

A={1, 2, 3}
B={1, 3}
C={2, 3, 4, 5}

Pertanyaan

a. A U B U C

Jawab
A U B U C={1, 2, 3, 4, 5}

b. A ∩ C

Jawab
A ∩ C={2, 3}

c. B ∩ C

Jawab
B ∩ C={3}

d. A - B

Jawab
A - B={2}

e. C - B

Jawab
C - B={2, 4, 5}

f. (C - B)’

Jawab
(C - B)’={1, 3}

g. C’

Jawaban
C’={1}

5. Jika diketahui data sebagai berikut.

A={1, 3, 5}
B={1, 3, 5, 7}
C={4, 5, 6}

Tentukan :

a. Gambarkan diagram venn dari A ∩ B ∩ C

Jawab :
A ∩ B ∩ C={5}

b. Gambarkan diagram venn dari B - A

Jawab :
B - A = {7}

Pada dasarnya, semua materi himpunan dalam matematika secara umum telah terangkum dalam satu artikel ini, secara khusus operasi dalam himpunan yang sering muncul dalam soal-soal yang berkaitan dengan himpunan. Sebagian besar materi himpunan, menggunakan anggota-anggota himpunan bilangan. Oleh sebab itu, anda sebaiknya mengenal jenis-jenis bilangan yang merupakan salah satu dasar penting dan utama dalam matematika.

Materi himpunan matematika ini terdapat pada pelajaran matematika kelas 8 SMP dan pada kelas XI SMA serta mata kuliah logika informatika dan beberapa bidang ilmu lainnya.

Demikianlah artikel materi himpunan lengkap dengan contoh soal dan jawaban. Pada artikel selanjutnya kita akan membahas tentang relasi dan fungsi yang merupakan materi lanjutan dari himpunan. Semoga bermanfaat!